정렬 알고리즘을 이야기하다보면, 항상 비교되는 두가지가 퀵 소트와 머지 소트이다. 일반적인 상황에서 두 정렬의 복잡도는 O(nlogn)으로 표기한다.
두 정렬을 구태여 비교하는 이유는 분할 정복(divide and conquer) 패러다임을 이용하기 때문이다. 임의의 배열이 있을 때 반으로 쪼개어 가면서 각 원소를 순서대로 배치하는데, 퀵 소트는 분할 이전 그리고 머지 소트는 분할 이후에 이를 순서대로 배치한다.
좀 더 쉽게 그림으로 보자.
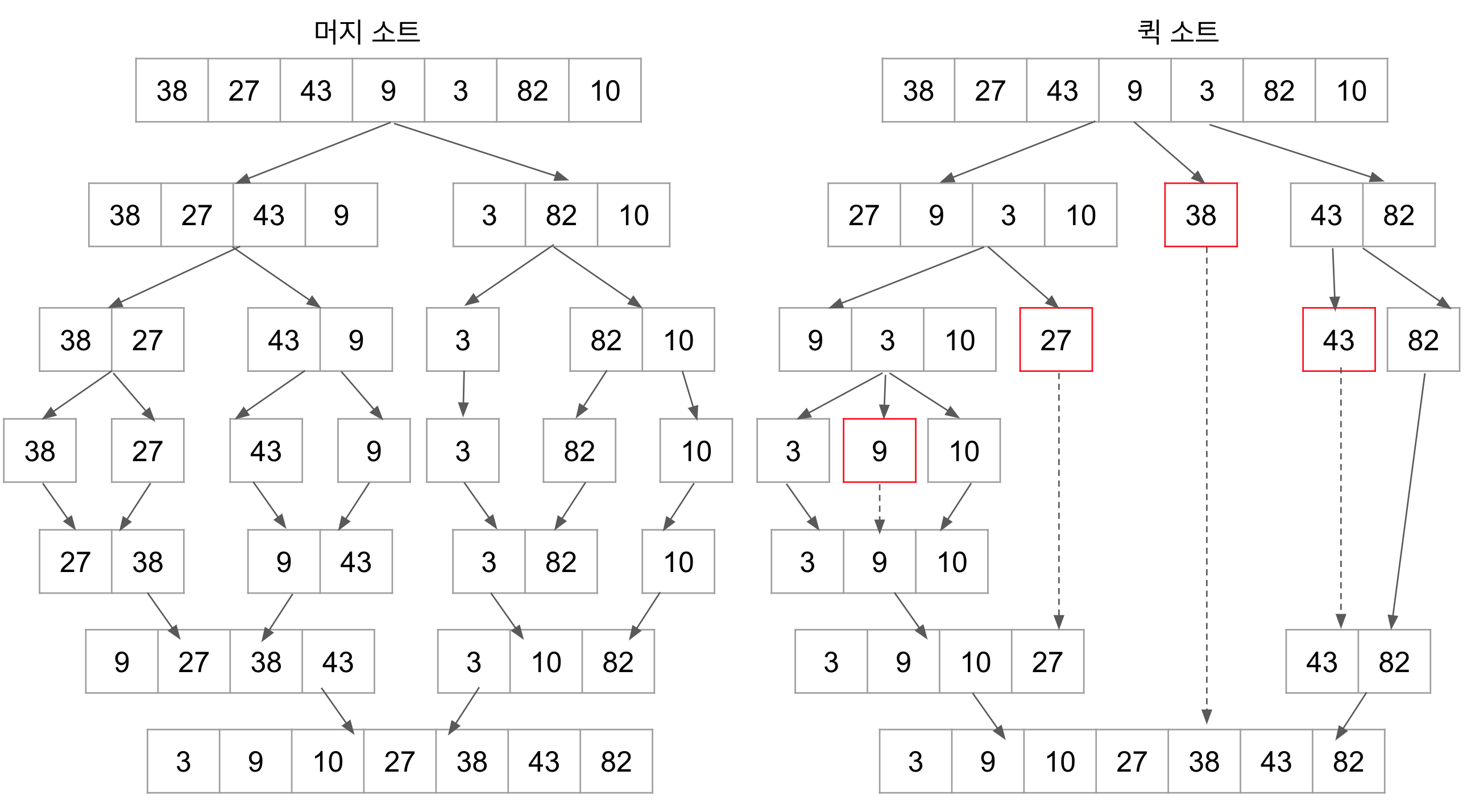
왼쪽 머지 소트는 배열을 1/2씩 나눠가면서 정렬이 되었을 때까지 계속해서 나누어간다. 만약 원소가 1개가 된다면 부분 배열은 정렬된 상태이므로 그 다음부터는 합쳐가면서 다시금 배열을 조립한다. 이 합치는 과정은 각 부분 배열의 길이와 같으므로 O(N)이 걸리게 된다.
반면 퀵 소트는 부분 배열의 최우측 및 최좌측 원소를 피벗과 비교하여 교체O(N)한다. 이후 각 원소를 가르키는 인덱스가 교차한 지점에 피벗을 위치시키고 다시 부분 배열으로 쪼갠다.
이처럼 퀵 소트는 부분 배열으로 나누기 이전에 O(N) 작업이 발생하며, 머지 소트는 부분 배열을 다시금 합치는 과정에 O(N) 작업이 발생한다.
이제 소스코드로 보자.
#include <iostream>
#include <cstring>
using namespace std;
int h[] = { 38, 27, 43, 9, 3, 82, 10};
int n = 7;
int temp[7];
void merge(int left, int right){
if(right-left == 1) return;
int mid = (left+right)/2;
merge(left, mid);
merge(mid, right);
memcpy(temp, h+left, sizeof(int)*(right-left));
int i = left, j = mid;
int k = 0;
while(i < mid && j < right){
if(h[i] <= h[j])
temp[k++] = h[i++];
else
temp[k++] = h[j++];
}
while(i < mid) temp[k++] = h[i++];
while(j < right) temp[k++] = h[j++];
memcpy(h+left, temp, sizeof(int)*(right-left));
}
void quick(int left, int right){
if(right-left<=1) return;
int i = left, j=right;
while(i < j){
do{
i++;
}while(i<right && h[i] < h[left]) ;
do{
j--;
} while(j>left && h[j] > h[left]);
if(i<j)
swap(h[i], h[j]);
}
swap(h[left], h[j]);
quick(left, j);
quick(j+1, right);
}
int main(){
for(int i = 0 ; i < n; i++)
printf("%d ", h[i]);
printf("\n");
merge(0, n);
quick(0, n);
for(int i = 0 ; i < n; i++)
printf("%d ", h[i]);
}
두 정렬이 코드는 [left, right)으로 작성되어 있다.
우선 머지 소트부터 보면, 길이가 1이면 정렬된 상태이므로 아무것도 하지 않는다. 이후 중간값을 만들고 다시금 부분배열에 대해 머지소트 함수를 호출한다. 이 경우 길이가 1인 배열들로 모두 쪼개어지고 나서 리턴되는데 이때 좌, 우 부분 배열에 대한 인덱스 i, j를 셋업한다.
그런 다음 각 인덱스 i, j가 부분 배열의 끝을 넘지 않는 선에서 둘중에 작은 값을 임시 배열에 담고, 만약 둘중에 하나가 먼저 끝났더라면 나머지 부분을 임시배열에 마저 담는다. 그런 다음 원 배열에 다시 복사한다.
퀵 정렬을 살펴보자. 퀵 정렬은 피벗을 가장 왼쪽으로 한다. 우선 길이가 1이면 머지소트와 마찬가지로 아무것도 할 필요가 없다. 여기서 부등호를 쓴 이유는 피벗의 위치에 대한 검증 없이 부분 배열에 대하여 quick 함수를 호출하기 때문에 Out of index를 방지한 것이다.
i, j를 배열의 좌, 우로 잡고 i < j 조건으로 루프를 돌린다. 이때 초기값을 left, right로 준 이유는 아래의 do-while문에 의하여 자연스럽게 피벗의 위치인 left와 배열의 끝 위치인 right가 생략되기 때문이다.
이제 각 좌우점에서 피벗보다 큰값과 작은값을 찾는다. 만약 i와 j가 만나지 않았다면 (i<j) 이 두개의 값을 바꾸어준다. 이렇게 계속해서 루프를 돌다보면, i와 j는 반드시 만나게 되며 그중 j 값은 피벗보다 같거나 크지 않은 위치에서 종료하게 된다. (반면 i는 항상 피벗보다 큰 값 또는 배열 밖에서 종료된다)
따라서 우리는 피벗과 j 인덱스가 가르키는 원소를 스왑한 다음, 피벗 좌우의 부분 배열에 대하여 퀵 소트 함수를 호출하여 준다.
'프로그래밍 > 컴퓨터 알고리즘' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리를 위한 Disjoint set과 크루스칼 알고리즘 (0) | 2019.05.07 |
|---|---|
| [알고리즘] 트리 순회 (전위, 중위, 후위)와 중위+후위 -> 전위 순회 찾기 (0) | 2019.05.07 |
| [알고리즘] 바이너리 서치 구현과 설명 (0) | 2019.05.03 |
| [알고리즘] 시간 복잡도 계산 / 마스터 정리 (0) | 2019.04.14 |
| [알고리즘] 시간 복잡도, 점근적 분석법 그리고 표기법 (0) | 2019.04.14 |





