시간 복잡도 계산, Master's theorem / 마스터 정리
1. 시간 복잡도
시간 복잡도란? 특정한 프로그램의 실제 동작 시간이 아닌, 입력 데이터의 크기 n에 대하여 기본적 연산의 횟수를 측정하는 것을 의미한다. 시간 복잡도를 표현하는 방법은 총 3가지가 있다.
- 최선
- 평균
- 최악
간단한 정리는 아래의 포스팅을 읽어보자. [알고리즘] 시간 복잡도, 점근적 분석법 그리고 표기법
2. 시간 복잡도 계산
시간 복잡도 함수 `T(n)`은 일반적으로 재귀 형태의 수식으로 주어지는데, `n=1`까지 모든 항을 구해서 그 합을 구하면 그 값이 시간복잡도가 된다. 예를 들어 가장 간단한 시간 복잡도 함수를 보면,
`T(n) = T(n-1) + n`
이 `T(n)` 함수는 1회 실행에 n번의 기본 연산을 수행하며, 다음에는 n-1개의 데이터에 대해서 재귀적으로 수행한다는 의미이다.
이 함수를 풀어써보면,
`T(n) = 1 + 2 + ..... + n-1 + n = sum(1, n)`
따라서 `sum(1,n)`은 등차수열의 합 공식으로 `n*(n+1)/2`임을 알 수 있고, 여기서 `T(n)= O(n^2)`을 알 수 있다.
3. 마스터 정리
마스터 정리는 특정한 시간 복잡도 함수에 대하여 빠르게 계산할 수 있는 수식이다. 따라서 어느 형태의 시간 복잡도 함수에 대해서는 적용할 수 없는 경우도 있다.

위의 수식은 마스터 정리를 적용할 수 있는 형태다. 총 3가지 경우에 따라서 계산하는 방법이 다르다. 이 케이스를 나누는 방식은 a, b의 값을 바탕으로 계산한다.
1번 경우
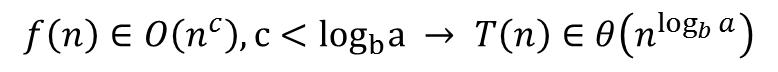
위와 같이 계산할 수 있다.
예를 들어 `T(n) = 4*T(n/2) + n` 이라면, `a = 4`, `b = 2` 이고 `log_b a = 2`이다. 이때 `f(n)`의 최고 차항이 1이므로 이 함수의 시간 복잡도는 `theta(n^2)`가 된다.
2번 경우
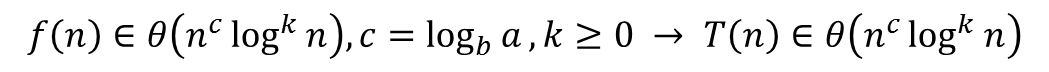
예를 들어 `T(n) = 2*T(n/2) + n` 이라면, `a = 2`, `b= 2`이고 `c = 1`이다. 따라서 시간 복잡도는 `theta(n log n)`이다.
3번 경우

예를 들어 `T(n) = 2*T(n/3) + n` 이라면, `log_b a` 는 `log_3 2` 이면서, `c=1`이다. 따라서 `c > log_b a`를 만족한다. 또한 `2*(n/3) <= k(n)`의 경우 `2/3 <= k < 1`을 만족하므로 시간 복잡도는 `theta(n)`가 된다.
4. 마스터 정리를 적용할 수 없는 케이스
사실 저 형태의 시간복잡도가 아닌 함수는 빠르게 해결 할 수 없다. 예를 들어 `T(n) = T(n/2) + T(n/4) + n` 인 경우가 그렇다. 이 경우는 트리 형태로 그려가면서 풀면 공비가 3/4인 등비수열의 합으로 나타낼 수 있다. 또한 멱급수나, 미적분을 해야하는 경우도 있으니, 사실 많이 풀어보는게 답이다.
'프로그래밍 > 컴퓨터 알고리즘' 카테고리의 다른 글
| [알고리즘] 퀵 소트와 머지 소트 비교와 구현 (0) | 2019.05.06 |
|---|---|
| [알고리즘] 바이너리 서치 구현과 설명 (0) | 2019.05.03 |
| [알고리즘] 시간 복잡도, 점근적 분석법 그리고 표기법 (0) | 2019.04.14 |
| [알고리즘] Convex hull과 Graham's scan (0) | 2019.04.14 |
| [알고리즘] Convex Set과 특징 (0) | 2019.04.10 |





